↖  理解计算：从根号2到AlphaGo -14: 第6季 多维的浪漫：统计学习理论与支持向量机-2..

最优分类器与理想的统计学习

在对于任意的数据集（X,Y）损失函数L以及联合概率分布p(x,y)，那么是否存在一个能将期望风险降到最低的最优分类器？

实际上，这个分类器是存在的，即贝叶斯分类器fb。

它是各种分类器中分类错误概率最小或者在预先给定代价L的情况下平均风险最小的分类器, 它的设计方法是按照贝叶斯决策理论进行设计的一种最优分类器。

我在本季中不展开讲解贝叶斯理论，大家只需要知道设计贝叶斯分类器的关键是要知道样本 x的各种后验概率密度函数，这些要求决定了在实际情况下贝叶斯分类器的实际使用范围很有限，因为后验概率密度函数几乎与联合概率密度函数一样复杂且未知。

在前面的例子中我们给定了一个分类器，并了解了这个分类器对应的经验风险和期望(真实)风险。

统计学习理论的目标就是在有限n个数据样本的情况下，学习某个分类器fn，同时需要证明fn的性能与与贝叶斯最优分类器fb性能的之间的差距可以通过某种方式逐渐接近。

例如在样本数趋于无穷的时候，我们学习的分类器fn的性能如果够无限接近贝叶斯分类器fb的性能。

在理论上来说，就是分类器fn在样本无限多时能以任意大的概率和任意小的差距逼近贝叶斯最优分类器的性能，且对联合概率分布p (x,y)没有任何假设，这是我们最理想的统计学习策略。

最优学习策略说明只要不断增加数据，就能使学习得到的fn的分类性能(风险)就能够逐渐接近最优分类器fb的分类性能 (风险)。

在这里我们依然采用风险来度量分类器的性能。然而这个目标依然非常严格，达到这个目标非常困难。

这是因为，我们的学习算法实际上只是从一个函数空间F(假设空间)中选择某个函数f，但是我们的这个函数空间F很大程度上可能并不包含贝叶斯分类器，那么理论上在这个空间中，(随着样本数目的增加)任何学习算法都不可能获得接近fb性能的分类器，如图所示假设空间2不包含贝叶斯分类器fb。

图4 无法学习到的最优分类器[1]

尽管可能无法学习到贝叶斯分类器，我们依然希望了解采用某种方式学习得来的分类器fn和贝叶斯分类器fb之间的差距到底在哪里？ 为了进一步了解，我们看下面的图：

图5 学习的分类器与最优分类器的性能差距[1]

橙色点是贝叶斯分类器fb，绿色点是我们的假设空间中最优的分类器fF,， 即可以看作是空间F分类器中使期望风险最低的分类器，灰色点是我们的学习算法在利用n个样本训练得到的分类器fn , fn∈F，此时相较于贝叶斯最优分类器fb，性能差距为：

在假设F给定的情况下，如果对任意的概率分布p(x,y)，学习算法均能够贝叶斯一致，那么这个学习算法具有全局一致性。

随着前提条件越来越放松，一致性的要求越来越高。别说贝叶斯一致了，就是在假设空间F中一致性实际上也并不容易实现。全局一致的算法看起来更难找到。

神奇的是，在1977年科学家们证明了一种最简单的K近邻算法(K-Nearest Neighbor,KNN)在K为无穷大时，全局一致。

这个算法非常简单，如果一个实例在特征空间中的K个最相似（即特征空间中最近邻）的实例中的大多数属于某一个类别，则该实例也属于这个类别。

这也从侧面证明了这个简单算法的强大之处，但是K为无穷大时的全局一致性只能是一种理论存在。

经验风险学习的性能

尽管我们介绍了fn和fF以及fb之间的关系，并且说明了学习方法应该具有一致性。但是依然忽略了采用哪种风险来学习得到fn。

实际上，我们手上只有经验风险看起来比较容易得到，如果利用经验风险最小化的方法(ERM)去学习fn，ERM学习是否能够满足一致性的要求，能够满足哪种一致性要求呢？

现在我们只考虑最宽松的一致性，即在ERM定义的经验风险Remp的情况下，随着样本数目n的增加，Remp(fn)是否能无限逼近F中期望风险最小的最优分类器R (fF)， 我们将看到，F空间的大小起到了很重要的作用。

单一函数假设空间|F|=1

在经验风险情况下，一种极端情况，在分类器的假设空间中只有一种选择f，那么无论何时fn=fF=f 都成立。显然，任何学习算法都能在F中一致。

我们现在关注的问题是，当n → ∞时，Remp(f) → R(f)吗？换言之，当样本增多时，f的经验风险Remp(f)是否可以无限逼近真实风险R(f)？

从之前经验风险和期望风险的定义可以看出，当f固定时，Remp(f) 是损失L的样本均值，真实(期望)风险R(f)是损失L的期望, 在n逐渐增多时，利用统计学中一个重要的定理：辛钦大数定律(样本数量很大的时候，样本均值和真实均值(期望)充分接近)直接得出结论：当f固定时，当n趋于无穷时，经验风险Remp (fn)可以依概率收敛到真实(期望)风险R(fF)。

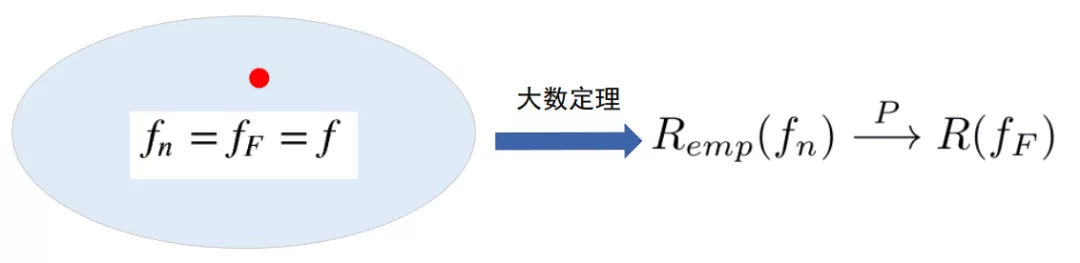
图6 单一函数空间中学习的一致性

 有限假设空间|F|=n

当F中有多个函数时，由于fn是一个依赖于样本集的非固定函数，大数定律失效，但是大数定理的基本思想是统计学习理论最核心的依据。

我们希望能将大数定律推广到假设空间是多个函数的情况。我们必须寻找一种统一看待多个函数的方法，即通过定义一个F中所有函数f的真实风险R和经验风险误差Remf的上界：

图7 有限函数空间中学习的一致性

 无限假设空间|F|=∞

当函数F的空间包含无限个假设的情况下， 问题看起来变得更加棘手。我们希望寻求一个办法，将无限个假设的情况通过一种转换，使其变成含有有限个假设的函数空间，然后就可以利用之前的结果。

(1)Symmetrization(平衡化)

在之前的介绍中，我们所有的一致性依赖f的真实(期望)损失R(f)。我们之前已经说过，真实风险是无法计算得到的，这是因为我们无法获得数据的分布，这个分布蕴含着无限多数据才能展现的信息，我们必须把这个东西用可观测的量替代掉。这时，我们需要一个叫Symmetrization的技巧。

简单来说，Symmetrization的意思是，如果我们除了Dn，还有一组独立于Dn且同样大小的iid抽样Dn'，定义其上的经验风险是Remp'(f)，则有如下定理(这个证明很复杂，我们只需知道结论即可)：

能够依概率收敛，那么fn的一致性也将得到保证。

上式将风险的一致性转换到仅仅依赖经验风险上，这种转换非常重要，因为在这种情况下， 即使F的空间大小是无限的，但是对于特定的n个样本(有限的)，经验风险的取值将是有限的。

(2) Shattering Coefficient (打散系数)

考虑一个二分类问题，给出一个有n个样本的样本集，不论你的F中有多少函数，最终输出最多只能有2n种可能（¨一个样本输出要么输出0，要么输出1）。

如果只考虑经验风险，任何F在面对n个样本时，在ERM评价下其等价于一个最多有2n个假设函数的有限假设空间(即n个样本最多有2n 种分法)。我们将问题从考虑无穷个假设的F空间转化为F对n个有限数据有限的分类结果上，这简直太棒了。

实际上，情况还要更好！现在我们要考察样本数为n时，F(包含有无穷的假设)所能给出的分类个数，我们将这个度量表示为N(F,n)，即F对n个样本产生的不同分类结果。

一个输入空间在[0,1]上的二分类问题：它选择一个点θ ∈ [0,1]，将区间分为[0,θ]和(θ,1]两部分，然后将两个部分分别作为一个类别。

简单来说，这个模型就是将输入空间一分为二，一边赋值为0，一边赋值为1，因为θ有无数种选择，所以F是一个无限集合。

可以看出，能输出的分类结果与样本点的个数相关。我们在下图展示了随着数据点个数的增加，分类模型所能产生的分类结果数目即N=(F,n)。其中垂直于坐标轴的箭头为分类器，红色箭头表示若样本在其左侧，则将其标记为0；同样蓝色箭头表示样本若在其右侧，则将其标记为1。

注意每一个时刻仅允许存在一个分类器。当n=1时，无论样本如何标记，总能把它分开。当样本个数为n=2时，无论样本怎样标记，只需要四个分类器就能把他们分开。

但是，当n=3时，数据样本的标记有8种情况，但是，分类器最多仅有6种输出(六个垂直的小箭头)。当n=4时，数据样本有16种标记情况，分类器最多能给出8个输出。

通过以上直观的分析，当[0,1]上有n个数据时，实际的标记有2n，我们的分类器最多有2n个输出。对于这个简单的分类模型，他的Shattering Coefficient 表示为

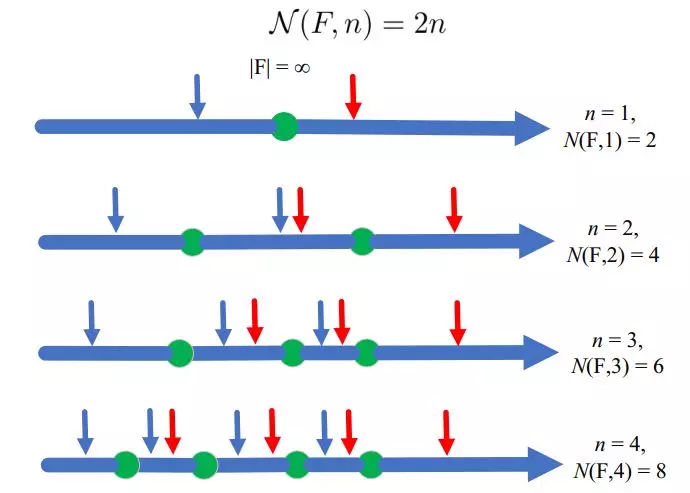
图 8 直线上分类模型的打散系数

Shattering Coefficient反映了模型随着n的增加，能够应对的输出的分类结果的个数。

基于在两个容量为n的样本集上，其经验风险差值的输出只有2^(2n)种可能，将F等价为一个容量为2^(2n)的有限假设空间。也就是说，我们把

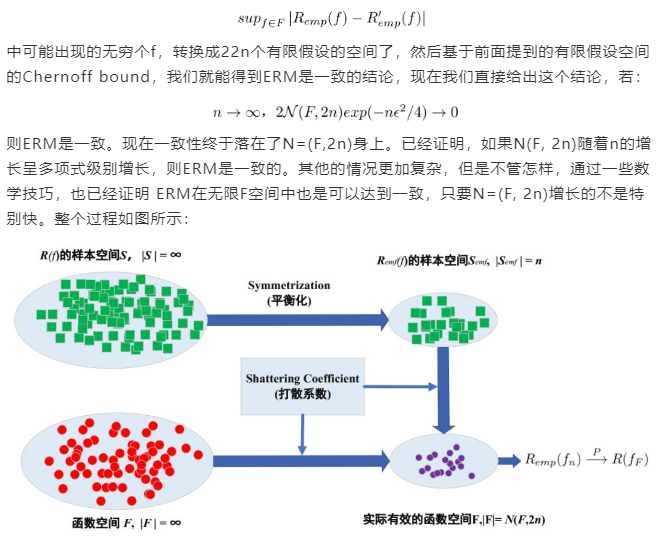
图 9 无限假设空间的一致性

经过漫长的历程，我们简要说明了ERM的一致性，这样我们就能对利用数据进行模型的学习有了基本的理论依据，我们终于明白，尽管假设可能有无穷个，只要它对数据的分类输出的能力并不是指数级增长的，或者说并不是能够对n个样本的所有情况都能输出分类标签的话，我们的学习就是有理论支撑的。

本页Url