↖  理解计算：从根号2到AlphaGo -11：第5季 导数的前世今生-2..

尽管关于微分比的概念不清楚，历史出版著作最多的数学家, 约翰·伯努利的学生欧拉在他的《分析学原理》中给出了很多微分之比，他已经意识到微分学的强大之处在于它同研究两个无穷小量的比值相关，尽管这个时候连他也无法明确什么是无穷小。

最为著名的微分之比就是它通过级数证明时y=sinx时，dy/dx=cosx。

当欧拉去世时，正是莱布尼茨发表第一篇微积分论文99周年，在这近100年的时间里，分析学取得了巨大进展。

在这一个世纪里面，数学家们对曲线的几何性质依赖越来越少，在级数的基础上，开始对函数的代数运算依赖越来越多，而且只限于特定函数的积分或者级数，对于一般意义上的连续函数或是可微函数并不重视[2]。

在这一百年，由于概念不清楚的无穷小量的存在，微积分的基础依然令人怀疑和难以理解。

有一些数学家尝试建立更加完善的基础，达朗贝尔提出了建立在“极限”概念上的微积分。

他把dy/dx看作是有限项的商的极限。

他将这个商表示成z/u，那么dy/dx就是假定z和u是实数，并且不断减少，比值z/u越来越接近的量。但是由于缺少对极限的明确定义，困境依然存在。

欧拉的学生，拉格朗日试图建立排除无穷小量，逐渐消失的量，极限等不明确的概念的微积分，他通过把f(x+i)表示成i的无穷级数的形式：

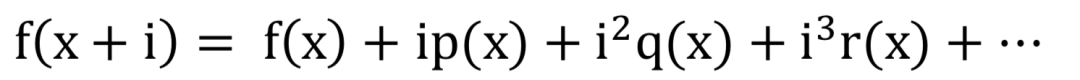
其中p，q，r..是从函数x得到的且与i无关的新函数。

这个级数就是泰勒级数，不过他认为这个级数再先，导数作为一种这个级数存在的结果。这样构造级数来寻找导数的方法的问题是无法保证这个级数能够收敛到原始的函数。

在欧拉去世后不久，一位在现代大学本科高等数学课本中举足轻重的人物，柯西诞生了。

这位处于古典微积分和现代分析学过度时期最著名的数学家，完善了工科高等数学现代教科书中绝大部分核心概念：极限，连续性以及导数。

在柯西之前，数学家们凭借着直觉和聪明才智取得了重大成就，在他之后，微积分的逻辑标准逐渐严格，从字面上看，分析学变得更加枯燥和不容易理解，同时也更加完备，无论是初学者还是数学家，几乎丧失了质疑的勇气。

柯西认为必须把全部微积分建立在极限的思想基础上，并且给出了相当经典的关于极限概念的定义：“当属于一个变量(数列或函数)的相继的值无限地趋近于(接近)某个固定的值时，如果最终同固定值之差可以随意的小，那么这个固定值就称为所有这些值(数列或函数)的极限。[2]” 

柯西的伟大之处在于在极限的定义上，避免提及如何达到极限或超过极限，而仅仅是通过引入一个随意小的值接近并保持接近它。

类似的他给出关于“无穷小量”的定义，当一个变量的连续数值无限减小(小于任何给定的值)时，这个变量就是无穷小量，实际上就是量的极限为0。

接着柯西开始考虑连续性。从函数y=f(x)开始,他令i为无穷小量，然后考察用x+i替代x时，函数的值，这个值的从y变为y+△y，也就是△y=f(x+i)-f(x),对于无穷小的的i，如果插值△y也是无穷小，柯西就称f(x)为x的连续函数。

这里无穷小的使用看起来字面上与牛顿的无穷小量和莱布尼茨的dx没有区别， 但是此时的无穷小已经建立在极限为零的概念之上了，这是微积分严格化历史上最为重要的工作之一。

19世纪60年代以后，魏尔斯特拉斯创造了ε-δ语言，对微积分中出现的各种类型的极限重新表达，就是我们所有人都学习过的高等数学课本中极限的定义(请对照查看同济版高等数学函数极限的定义)：

一句话，ε-δ是一种精确描述极限(无限接近某个值)的数学语言，这种数学语言的思想由柯西提出，最终由魏尔斯特拉斯完成定义。

从此以后，对于没有思想准备的数学门外汉而言，数学建立了一道形式化的门槛。

1840年，当中国陷于鸦片战争的境地时，在世界范围内的数学领域中，没有人不知道柯西。

1859年，大清帝国著名的数学家李善兰与汉学家英国人伟烈亚力(Wylie Alexander,1815~1887)合作翻译了美国数学家E·罗密士（Elias Loomis，1811-1889）的《解析几何与微积分》出版，取名《代微积拾级》，这是是西方微积分著作的第一部中文译本。

不久之后，这本书传到日本，第一次将欧洲数学带入日本数学界。今天我们熟悉的高等数学中很多的名词，“微分”，“积分”，“函数”，“级数”，“极大”，“极小”，“方程式”，“全微分”，“曲率“，”曲线”以及“横轴纵轴”等大都来自于这本创世的译作。

中国文化的博大精深从这些译文中你也应该深有体会，现在我们再也找不到比这些更完美的译文了。

尽管柯西的研究对现代分析学产生了重要影响，然而他的积分仅限于连续函数，对数学精确性的权威解释还要，再半个多世纪的等待，因为那个时候，关于实数，这个数学家经常使用但是却对其根本性质依然不清楚的概念继续得到完善，随着与集合论的结合，分析学也彻底的改变了其自身的面貌。

时间进入到二十世纪，我已无法对分析学完备的过程做更多的解释(主要是泛函分析没学好)，20世纪上半叶，分析学经过黎曼，魏尔斯特拉斯的不断严格化，随着实数的完备性逐渐清晰， 最终由勒贝格把微积分严格化的革命带入到实分析这一现代分析学领域。

简单的说，就是他定义了称之为勒贝格积分的东西使得积分能够在更广阔的领域开展工作，而不仅仅限于连续函数，他的积分更具有普遍性。

除了微积分，莱布尼茨兴趣广泛，也是自动计算最早期的思想来源，他提出了通用编码语言，用素数表示主要概念，从而形成一个数字和思想的完美映射，同时他把二进制编码看作是通用编码的关键，并从中国易经的卦象中得到二进制表示的灵感，还给出了10进制和2进制之间转换的方法[3]。

人类智能的一个关键特征是“无限使用有限方法”的能力，其中一小部分元素可以以无限的方式有效的组合在一起，人类的语言和文字就是典型代表，当然也包括莱布尼茨提出的极简到0-1的二进制。

时间是如此的巧合，在二十世纪上半叶，人类历史上最伟大的理论成果微积分经过两百多年得历程完成了它严格化的历程。而就在不久之后，同样，在莱布尼茨伟大思想的指引下，在普林斯顿高等研究院的冯诺依曼与他的同事撰写了《电子计算机逻辑设计初探》（Preliminary discussion of the the logical design of an electronic computing instrument），最终实现了莱布尼茨在数字计算和通用语言方面的梦想[3]。

尽管当时电子计算机那时刚刚来到这个世界。从理论上而言，导数已经变得不在让人不安。

计算导数的任务则像其他繁琐的事务一样，开始由人工转向借助于计算机了。我们逐渐清楚的了解了导数的历程。现在是时候看看导数的威力，并寻求一些更好的求导方法了。

2 导数的作用

在牛顿和莱布尼茨还要更早一些，大约在1629年，法国数学家费马研究了作曲线的切线和求函数极值的方法；从一开始，导数就与极值问题联系密切。

由于当时连函数的概念都不清楚，因此更多的从几何角度谈论函数，也就是曲线。

曲线在某一点的导数，则形象化的被看作是在这一点上切线的斜率。

导数的变化实际上反映了函数(曲线)的形态上的变化。

而且我们一般在实际使用过程中，更加关注那些位于特定形状端点的那些值。

现在假设有一个函数y = f(x)，当f′(x) = 0，当的时候,表明在这一点x的斜率为0，f′(x)的点称为临界点或驻点。

临界点除了局部极小点(local minimum)、局部极大点(local maxmum)外，还有鞍点，鞍点(saddle points)既不是最小点也不是最大点, 如下图9所示：

图9 斜率为零的三种临界点[5]

在这种简单情况下(函数有具体形式且能够得到导数)， 通过求解导数为零的点，就能相对比较容易的得到函数的极值点。

如果我们能够得到这些临界点，那么函数的基本形态也就在我们的掌控之中了。使f(x)取得全局最小值的点是全局最小点。

只有一个全局最小点（global minimum）或存在多个全局最小点的函数是有可能的。一般的情况则是存在不是全局最优的局部极小点，这种情况更加常见，如图10所示。

图10 存在多个局部极小点的情况[5]

然而，不幸的是，直接利用该方法计算导数去寻找函数的极值点在一些更复杂的情况下几乎没什么用处。特别是函数变量过多的话那就是噩梦。为了更清楚的看清这个问题，可以看看下面的多层感知机（MLP，实际上MLP的激活函数不是感知机的阶跃函数而已经变成了S形的Sigmoid函数，但是由于历史原因，依然称之为多层感知机)：

图11 多层感知机[4]

在前一季中，我们已经知道明斯基已经认识到多层感知机能够解决XOR问题，但根本原因是无法找到一个可行的寻找多层感知机参数的方法。

实际上多层感知机（甚至所有的神经网络）本身是一个复合函数，表示为f(.)，最重要的一点是，根据端到端的学习的基本思想，我们希望⽹络(函数的另一种说法)的输出f(x)能够满足所有数据本身的响应，这个时候我们就认为网络学习好了，可以用来进行处理数据了。

就跟我们在第一季介绍感知机时说的那样寻找直线（f(x)）来分类一样，错分样本会产生代价，此时的目标不过是稍微复杂一些罢了，为了量化我们如何实现这个⽬标，我们这里也定义⼀个简单的代价函数：

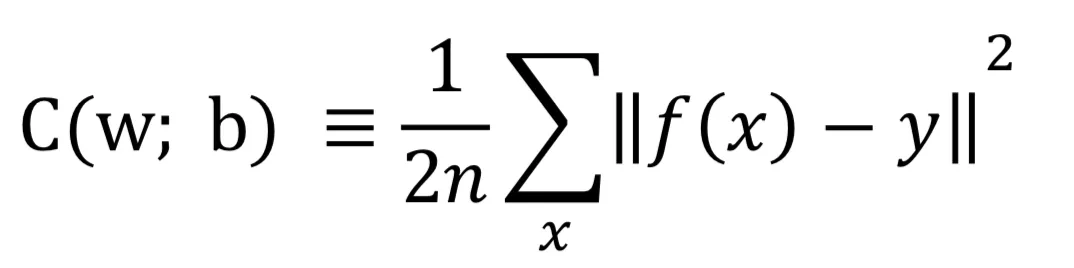
这⾥ w 表⽰所有的⽹络中权重的集合，b是所有的偏置,n是训练输⼊数据的个数,f(x)是表⽰当输⼊为 x 时网络的输出，y表示x对应的实际类别，求和则是在总的训练输⼊x上进⾏的。

代价函数没有什么特殊和神秘，本质上是为f来拟合x和y之间的对应关系寻找一个量化的标准罢了，代价函数的基本原则就是希望输出与本身的标记或者期望的响应接近。因此，我们将会看到，大部分代价函数样子很类似。

当然，输出f(x)取决于x, w和b，但是为了保持符号的简洁性，我没有明确地指出这种依赖关系。因此如果我们能找到合适的权重和偏置，使得C(w; b)≈0，则表明f(x)比较好，我们就有较高的信心让f来处理未知的数据x’。

相反，当C(w; b)很⼤时那意味着对于⼤量地输⼊， y 与输出 f(x) 相差很⼤，这种映射关系肯定不是我们想要的。

因此我们的⽬的，是最⼩化代价函数 C(w; b),具体来说就是寻找复合函数法f(x)中w，b的值，使得对于已知的训练样本x和其标记y产生的代价C(w; b)最小。

本页Url