当时的计算机科学，并没有多少大数据的概念，那时只要能解决逻辑运算的问题，这个机器就威力无穷，就像MP模型一样。

但如上一季看到的那样， MP模型的问题在于必须人工设计参数，才能完成复杂运算。罗森布拉特的感知机更加雄心勃勃，他宣称可以通过机器自动学习来实现很多操作(识别,运算,处理等)，当然得包括简单的逻辑运算了。

实现这种运算，也并不需要人为设计，只需要把数据(事件)摆在这里，让机器自己学习，然后，感知机就可以作为一种最简单的逻辑运算器了。

例如，为了实现与运算，我们只需要把与运算的输入和输出看作条件反射就行了,为了与麦卡洛克和皮茨得MP对比，我们将给出用感知机模拟“与门”的方法。

首先“与运算”的规则很简单，对于所有的二元逻辑运算，总共就只有四种输入，分别对应于p1-p4这四个二维向量，向量的每一维表示了二元运算的一个输入，运算结果根据运算的定义而不同，在“与运算”的定义下， 运算结果的输出t1-t4也可以看作是这对输入的标记，如图6所示。

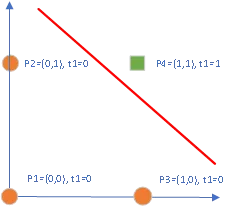
图 6 感知机实现的与逻辑运算

对这个明显的线性可分问题而言，感知机得心应手，很快就能找到这样的直线，此时的直线就是一个与门运算单元。重要的是得到这条直线是如此的简单，几乎都是自动化的。

依然有可爱的同学会觉得纳闷，既然与运算的规则这么简单，为何还要这感知机? 感知机去做这些确实有点牛刀杀鸡的感觉，但是仅仅通过数据或事件的训练来构造一个逻辑门的方法在那时可真是开天辟地的大事。

你可以想到那些在平面上可以线性可分的逻辑门（例如，或门）都可以用感知机来模拟。

遗憾的是，异或门(XOR)对于罗森布拉特的感知机就没那么简单了。明斯基和帕普特就以此为例给了感知机致命一击，在这个问题中，数据与之前类似，pi表示向量，ti表示它对应的输出标记，可以看到，p2和p3是一类，p1和p4是一类，如图7所示。异或运算是实际上可以看作是二进制的不进位加法，因此意义非凡。

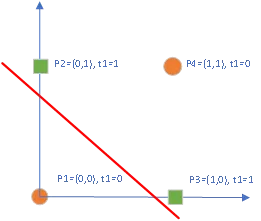
图 7 感知机无法模拟的异或(XOR)运算

不用多说，这两类数据根本无法用一条直线把他们分开，感知机在这里完全不起作用。对这个简单的异或问题，感知机看起来几乎彻底失败了。

实际上， 在当时，很多人已经知道，简单的感知机确实存在这样的问题，尽管明斯基和帕普特也承认，几层相互连接的神经元能做的可能够多，但是他们找不到研究这些神经元的方法，其他人也一样。

现在我必须不情愿的再次给出感知机相对严格的表达，从而才能看出它的问题所在，以及困难之处。在这里我将给出它与MP模型以及Hebb学习规则之间的关系。

罗森布拉特的感知机表示的神经元与麦卡洛克和皮茨的神经元几乎一样，只是缺少了一个控制信号I(请参考第三季神经元的数学模型)。单个神经元本身也可以看作是一个激活函数g(z)。

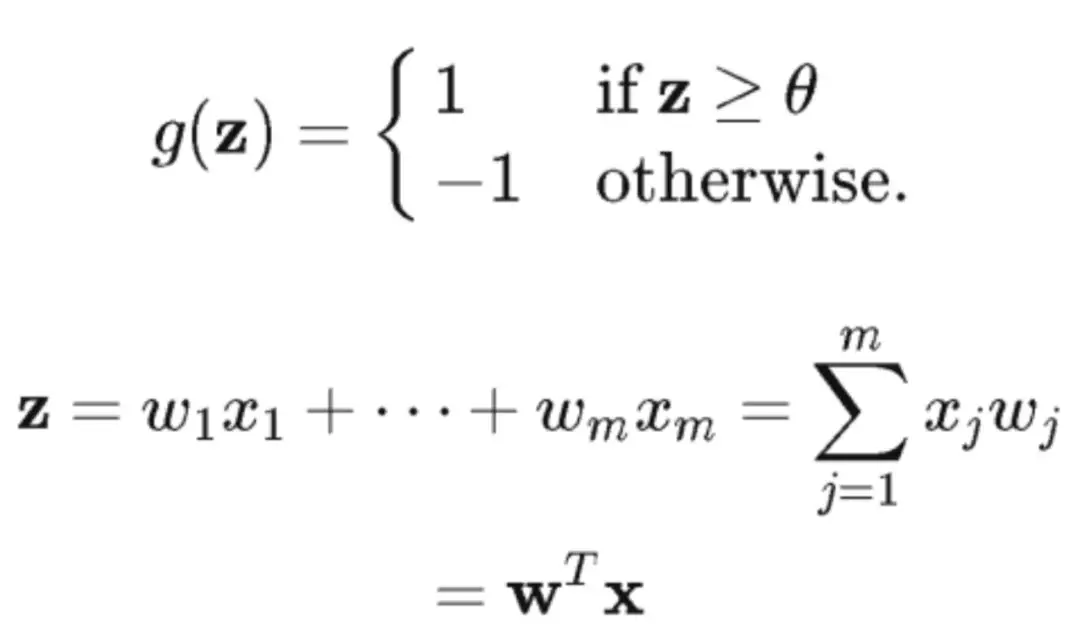
x1,...,xm是输入，w1,...,wm则是权值，注意上面的式子里有一个θ，激活函数本身的定义就反映了神经元的“全或无法则”。为了让这个式子更加简单，可以把阈值θ进一步放在z的一边，并定义，w0 = -θ 以及 x0 = 1, 这样，上面的式子变得更加整齐:

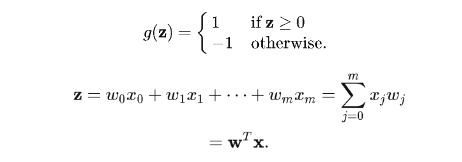
此时，感知机本身从结构上可以表示成如图8所示的一个神经元：

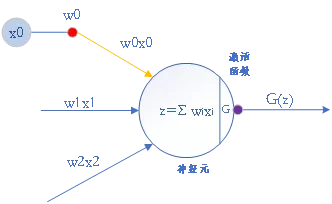
图 8 用神经元表示的感知机

我们需要再一次强调，感知机的伟大之处在于它给出了一个自动获得w的学习规则，这个学习规则：

1）首先随机的初始化一个w值

2）对每一个样本xi，计算当前的激活函数值g(z)=g(w^Txⁱ)，然后根据g(z)的值进行更新。

具体而言，g(z)的输出记作outputi,感知机利用outputi与xi本身的标记targeti之间的关系来更新w。更新w的规则反映了罗森布拉特的天才智慧，更新规则如下：

这个规则与 Hebb 学习规则形式上有些类似，只是将 w 以及xi的标记引入到了更新规则中，这个规则保证了只有错分样本能够更新直线的参数 w。

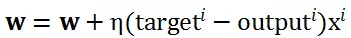
尽管感知机只能在两类样本线性可分的情况下找到这条直线，但是并不是说它在线性不可分的时候一无是处，如果两个类不能被线性决策边界分隔，我们可以设置一个迭代次数(epochs）和/或一个阈值，用于容忍错误分类的数量。

实际上，这个技巧是目前所有深度学习必须掌握的，因为他们面临与感知机几乎一样的尴尬情景，线性分类器无法解决线性不可分，而深度学习无法找到最优解，他们不能自己停下来，必须人为的进行干涉。图9给出了迭代多次的感知机如何应对线性不可分的问题。

图9  感知机处理线性不可分问题

1960年，斯坦福大学的Bernard Widrow和它的博士生Ted Hoff在MP模型和感知机的基础上，提出了一个称之为自适应线性神经元: Adaptive Linear Neuron (Adaline)的模型[15]，这个模型比感知机更接近现在的神经网络，更加重要的是，这个模型为下一步为20多年后神经网络的复兴埋下了伏笔。

这个神经元与感知机非常相似却又有明显不同，如下图10所示[16]：

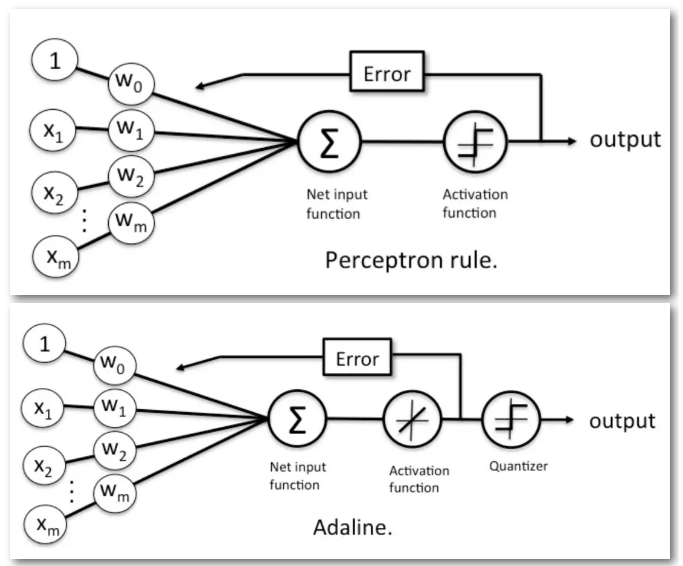
图 10 感知机(上图)和Adaline的学习规则[16]

结构上看，它增加了一个量化器来保证输出满足要求。另一方面，为了让参数w能够更新，它引入了一个可微的线性激活函数来替代感知机的阶跃激活函数。

这个可微的激活函数导致的结果就是，由这个激活函数，可以定义一个评价w值性能好坏的代价(误差)函数，从而让寻找w变成了一个简单的优化问题。

千万不要小看个微小的改变，这个可微的代价函数的引入却几乎使现在的深度学习再也逃不出这个框架了。最小化代价函数也是其他类型机器学习算法的主要思想。

Adaline引入的代价函数非常简单，就是最常见的均方误差函数(Sum of Squared Errors ：SSE)：

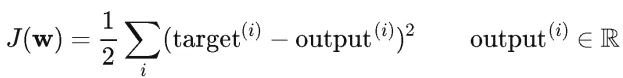
这个均方误差的含义也十分明显，对给定的一个 w，希望所有的样本都能满足自身的标记target 和模型的输出 output 一致。如果代价 J 比较大，则修改 w 让 J 变小。

平方的引入使得这个函数 J 本身变成一个凸函数（凹函数？）。我们可以使用梯度下降(gradient descent)的方法来解决这个问题，根据梯度下降方法的基本原理(由于篇幅原因，我们将在后面的文章中详细介绍这个原理的背景知识)，该过程可以描述成如下的一个图形[16]，w 只要沿着 J(w)在 w 的梯度的相反方向移动，就可以让 J(w)的值下降，当 J(w)关于 w 的梯度下降到零(或者接近零)的时候，意味着 J(w)达到了一个局部最小值，如果 J(w)是一个凸函数，则局部最小就是全局最小。

图11 代价函数J的梯度下降方法[16]

注意，此时w变成了代价函数的参数，我们的优化问题的目标是寻找J达到最小值时对应的参数w，而不是J的最小值本身。每一次更新的w可以看作求解根号2时的一个新的猜测，不过这个猜测依赖J关于w的梯度罢了。更具体一点，我们先考虑J(w)在一个方向上的偏导数。

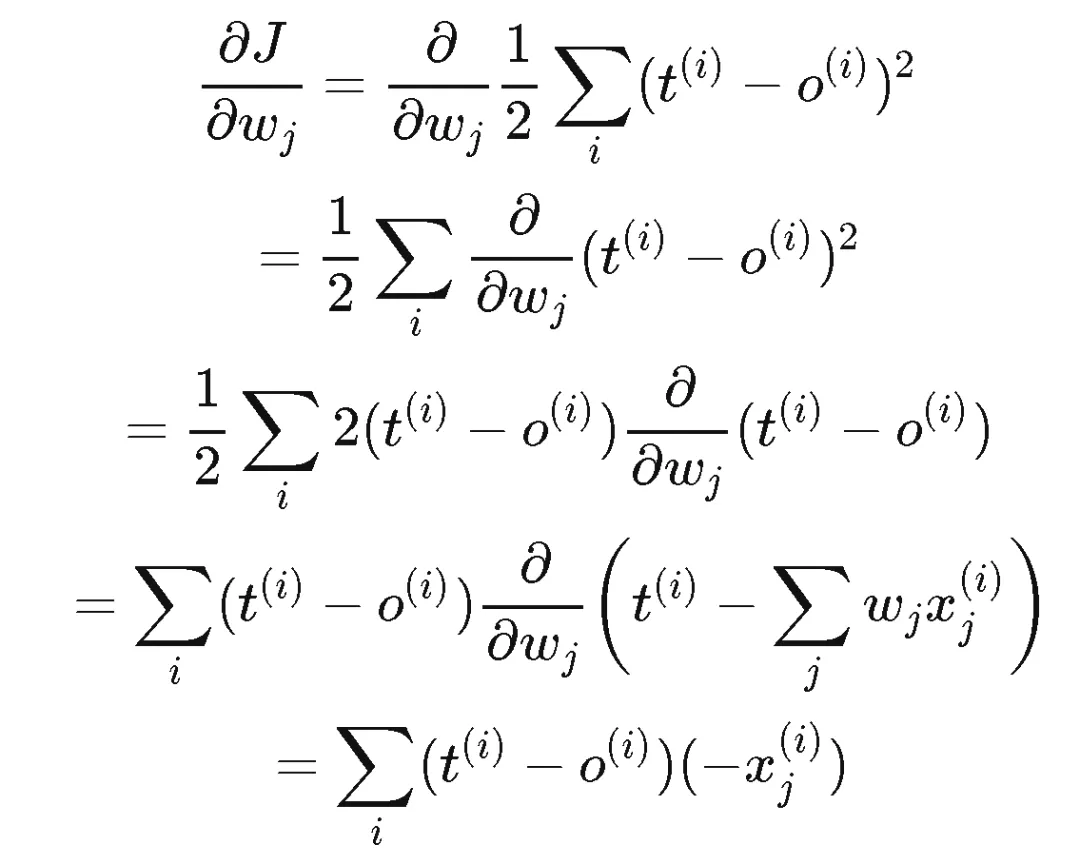
其中，(t = target, o = output), 根据梯度下降的学习规则，在这个方向上可以得到：

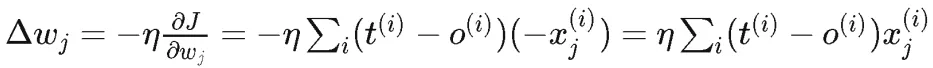
在不同方向上的偏导数构成的向量就是梯度，Adaline的更新规则如下：

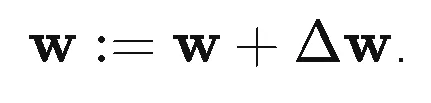
其中，∆w表示J关于w的梯度向量的相反方向，非常巧合地是,单从形式上看，感知机的更新规则跟Adaline看起来很像，但是o的含义不同， 在感知机中， o就是激活函数的输出，它只有两个值1，-1。而在Adaline中，o是一个实数。

同时，注意到Adaline的J(w)实际上依赖所有的样本的整体结果，而在感知机中， 每一次更新，只依赖一个样本。因此，如果你非得把感知机得更新也看成是J(w)的梯度下降的话(实际上是不能这么认为，因为感知机根本没有代价函数梯度下降的思想，而是直接给出了w的更新规则)，它则是类似随机梯度下降（ stochastic gradient descent）方法,该方法每次只利用一个样本来计算梯度，而Adaline属于批量梯度下降(batch gradient descent)方法，该方法需要利用所有样本来计算梯度。

Adaline通过引入代价函数，利用了早已经提出的梯度下降方法来解决优化问题，实际上Adaline也可以改进成随机梯度下降，这样就跟感知机更加相似了。但是他们的之间依然存在本质的不同，原因就在于线性激活函数以及代价函数的引入。

从形式上看，他们还是太像了，很多人都认为感知机可以直接写成梯度下降的形式，然而这是Adaline的功劳。按照我们第一季给出的计算的流程， Adaline的流程图如下所示,其中是用来表示梯度的通用记号。

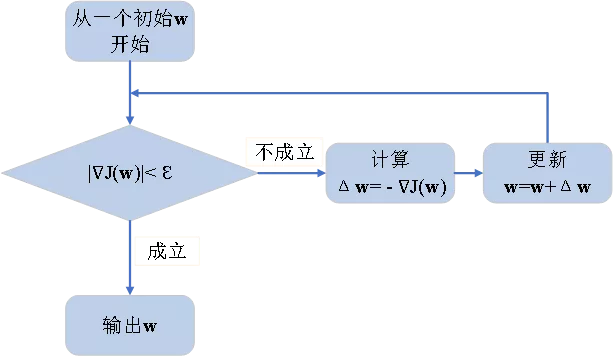
图12  Adaline引入代价函数和梯度下降的学习规则

以上的流程非常重要，几乎是到目前为止所有深度神经网络都共同遵守的流程。

然而，由于Adaline和感知机本身的样子还是一条直线，它们存在一样的致命问题，都无法解决线性不可分的情况。

1969年，当魔鬼搭档出版那本《感知机》后，这种线性分类器的日子都不太好过。

那么到底如何解决线性不可分问题呢？明斯基和帕普特特别指出需要多层感知机——亦即现在所谓的多层神经网络——才可以完成这一任务，罗森布拉特的感知机被认为是单层感知机，也有看作双层的(下图左)，这取决于你怎么看待它。然而三层及以上的神经网络就像下面这个样子(下图右)。

在多层神经网络中，多个感知机的输出作为另一个感知机的输入。

关键的问题是罗森布拉特的学习算法对多层并不管用，Adaline的方法也不管用。

那些处在多层神经网络中间层(隐含层)的神经元的权值(w1)，在当时无法进行调整。

因为感知机和Adaline只有两层，他们直接建立了输出层对参数w是如何影响的，并确立了简单的更新规则，但是对多层网络而言，实在是很难想到网络的输出对隐含的层中参数w1的影响。

这种困难在Aadline看来，就是无法容易的求出多层神经网络中代价函数对于所有参数w (w1及w2)的偏导数。这个问题对当时以及后来很长一段时期的人们，都是很困难的。

在《感知机》出版后的十多年，也几乎没人(实际上有但被忽略了)找到一个比较好的求导数(梯度)的方法。

连明斯基都以挑衅的口吻在书中写道：“证实(或推翻)把感知机推广到多层这个想法是没有希望的这一看法将是一个重要的研究内容。”

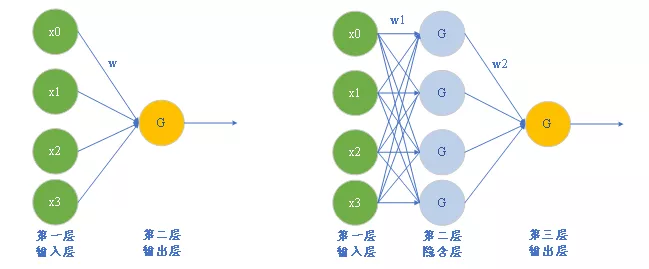
图13 看作2层神经网络的感知机(左图)和多层感知机

1973年，英国科学研究委员会请一位叫James Lighthill的数学家[17]撰写了一份关于人工智能研究的评估报告，在这份著名的“Lighthill Report”中， Lighthill对诸如人工智能中的机器人技术和语言处理等基础领域的基础研究提出了强烈批评，并给出最终结论：

“迄今为止，AI各领域的发现并没有带来像预期一样的重大影响” [17]。

这为英国政府大范围终止对人工智能研究的决定奠定了基础。这份报告意味着从1974年开始，人工智能的研究进入漫长的冬季(AI Winter)。

令人惊奇的是，就在1974年，哈弗大学的博士生Paul J. Werbos在他的博士论文《New Tools for Prediction and Analysis in the Behavioral Sciences》[18]中，详细描述了如何利用误差的反向传播来训练人工神经网络。

然而哈弗毕竟不是MIT，这篇经典的文献在当时并没有引起太多反响，因为冬天已经来临，很多人工智能的研究人员得不到资助，甚至论文也无法发表。

没有多少人意识到这篇文章的重要价值，这种情况除了得感谢《感知机》以外，就要数Lighthill的报告了，难以置信的是这两个文献的封面竟然如此相似！

然而，罗森布拉特甚至没有等到1974年。在1971年7月11日，在43岁生日的那一天，罗森布拉特在划皮艇的时候丧生。据说可怜的他连遗体也没有找到。很多人怀疑他是自杀，甚至一些人将他可能自杀的原因归结为《感知机》这本书给他带来的压力。在他去世前不久，还有一项不为多少人了解的重要发现。

1971年罗森布拉特在一个关于天文学的期刊《ICARUS伊卡洛斯》上发表了一篇文章，探讨了如何通过测量其他恒星的星光，来寻找这些恒星周围的行星[19]。

如果一颗行星从恒星和你的望远镜之间经过，你会看到光的强度略有下降。在此之前，天文学家大都尝试用天体测量的方法寻找行星，也就是测量由于行星引力导致的恒星位置的变化。

罗森布拉特的这篇文章，在同一年被比尔•博鲁茨基发现，这坚定了博鲁茨基利用光学技术以及望远镜寻找行星的工作。博鲁茨基和他的同事们持续完善改进罗森布拉特的方法，作为著名的开普勒太空望远镜(Kepler)项目的提出者之一、首席科学家，比尔•博鲁茨基发起的开普勒探测器计划从2009年开始对银河系内10万多颗恒星进行探测，希望搜寻到能够支持生命体存在的类地行星。

2015年，开普勒的最新成果是确认了第一个与地球近似大小、围绕一个类太阳恒星运转、公转轨道位于宜居带内的行星Kepler-452b。 在不可预见的将来，如果人类在宇宙中成功寻找到了智慧生物或与地球一样适宜人居的星球，我们也要铭记这位为人工智能做出杰出贡献且英年早逝的科学家。

尽管神经网络的研究进入寒冬，被人忽略的1974年反向传播思想的提出预示着一定会有另一些人在另外的合适时间及场合重新发现这个神经网络的救命稻草。

我们还会看到一些学者的坚持，使得这个漫长得冬天并非那么寒冷，就像大家经常说的那样，冬天来了，春天还会远吗？

参考文献：

[1]Donald_O._Hebb,https://en.wikipedia.org/wiki/Donald_O._Hebb 

[2] 佩德罗·多明戈斯，终极算法：机器学习和人工智能如何重塑世界，中信出版社，2017年1月

[3] 尼克，人工智能简史 人民邮电出版社，2017.12

[4] 伊万·彼得罗维奇·巴甫洛夫，https://baike.baidu.com/item/伊万·彼得罗维奇·巴甫洛夫

[5] 圣地亚哥·拉蒙-卡哈尔，致青年学者，新华出版社，2010年。

[6]Marvin Minsky , https://en.wikipedia.org/wiki/Marvin_Minsky

[7] Leslie Lamport , https://en.wikipedia.org/wiki/Leslie_Lamport

[8] 马跃 译 编程语言原理 第10版 清华大学出版社 2013年

[9] Joseph Marie Jacquard, https://baike.baidu.com/item/Joseph

[10] 王安, https://baike.baidu.com/item/王安/4457

[11]  Rosenblatt's Contributions. csis.pace.edu.

[12] John McCarthy https://en.wikipedia.org/wiki/John_McCarthy_(computer_scientist)

[13]  New Navy Device Learns By Doing. nytimes.com.

[14] Minsky, Marvin; Papert, Seymour. Perceptrons: An Introduction to Computational Geometry. MIT Press.

[15]  1960: An adaptive "ADALINE" neuron using chemical "memistors"

[16] Sebastian Raschka , Single-Layer Neural Networks and Gradient Descent http://sebastianraschka.com/Articles/2015_singlelayer_neurons.html

[17] James Lighthill , https://en.wikipedia.org/wiki/James_Lighthill

[18] Werbos, P.. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. PhD thesis, Harvard University, 1974

[19] Andrew Grant，送望远镜上天，去寻找外星行星！

https://www.guokr.com/article/425871/

本页Url