真正的創業投資高手都是贝叶斯主义者-10

十、写在最后：可纠错的反馈闭环，串起人生的项链

可纠错的反馈闭环，对个人而言是非常重要的关键思想。 

我认为，其底层是一种贝叶斯更新的哲学。 

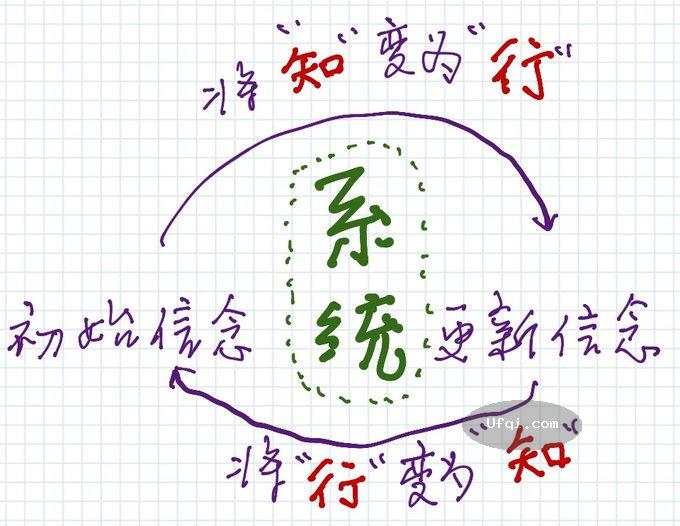
反馈闭环基本上是一种连续的过程，包括以下步骤：执行一个动作、观察结果、理解反馈、更新策略、再执行新的动作。

  在这个过程中，"理解反馈"和"更新策略"的步骤，就是在进行贝叶斯更新。

由于时间的推进，在我们的人生当中，每个反馈闭环并不是原地打转，而是犹如链条般串起来。

所谓有算法的人生，就是以   “可纠错的反馈闭环”为珍珠，串起不断更新、有复利效应的一生。

  我们要小心别断链子，也要避免一条链走到黑。 

如何成为一位贝叶斯主义的高手？ 那么，就让我用一句话体现：

笨蛋，行动起来！ 不管你有多害怕！  

----

贝叶斯定理（英语：Bayes' theorem）是概率论中的一个定理，描述在已知一些条件下，某事件的发生概率。

比如，如果已知某种健康问题与寿命有关，使用贝叶斯定理则可以通过得知某人年龄，来更加准确地计算出某人有某种健康问题的概率。

通常，事件A在事件B已发生的条件下发生的概率，与事件B在事件A已发生的条件下发生的概率是不一样的。

然而，这两者是有确定的关系的，贝叶斯定理就是这种关系的陈述。贝叶斯公式的一个用途，即透过已知的三个概率而推出第四个概率。

贝叶斯定理跟随机变量的条件概率以及边际概率分布有关。

作为一个普遍的原理，贝叶斯定理对于所有概率的解释是有效的。

这一定理的主要应用为贝叶斯推断，是推论统计学中的一种推断法。

这一定理名称来自于托马斯·贝叶斯。

贝叶斯定理是关于随机事件A和B的条件概率的一则定理。

P(A∣B) = [P(A) * P(B|A)] / P(B) 

其中A以及B为随机事件，且P(B)不为零。P(A|B)是指在事件B发生的情况下事件A发生的概率。

在贝叶斯定理中，每个名词都有约定俗成的名称：

P（A|B）是已知B发生后，A的条件概率。也称作A的事后概率。

P(A)是A的先验概率（或边缘概率）。其不考虑任何B方面的因素。

P(B∣A)是已知A发生后，B的条件概率。也可称为B的后验概率。某些文献又称其为在特定B时，A的似然性，因为P(B∣A)=L(A∣B)。

P(B)是B的先验概率。

按这些术语，贝叶斯定理可表述为：

后验概率 = (似然性*先验概率)/标准化常量

也就是说，后验概率与先验概率和相似度的乘积成正比。

本页Url