↖  计算机程序设计艺术（卷2）：半数值算法-3：第三章 隨機數..

第三章 隨機數

当然，任何想用算术方法生成随机数字的人都是在犯错．

——冯• 诺依曼（1951）

给出概率，以免别人怀疑你说假话．

——约翰• 盖伊（1727）

并不需要什么亮光引领人们运用他们的随机本领．

——约翰• 欧文（1662）

----

3.1 引言

在许多不同类型的应用中，“随机选取的”数都是有用的．例如：

(a)仿真．使用计算机模拟自然现象时，需要使用随机数使得效果更加逼真．仿真涵盖许多领域，从核物理研究（粒子服从随机碰撞）到运筹学（例如人们相隔随机的时间间隔到达机场）．

(b)抽样．通常，考察所有可能的情况是不切实际的，但是借助随机样本，我们可以理解“典型”行为．

(c) 数值分析．人们已经借助随机数，发明了一些精巧的方法，用于解决复杂的数值计算问题．关于该主题已经出版多部专著．

(d) 计算机程序设计．为检测计算机算法的有效性，随机值是很好的测试数据．更重要的是，随机算法离不开随机值，而随机算法常常比确定性算法有用得多．在这套书中，随机数的这种用法是我们最感兴趣的应用．正因为如此，我们在第3 章就研究随机数，然后才介绍其他大部分计算机算法．

(e) 决策．据报导，许多管理者都通过掷硬币或投飞镖等来做决定．谣传有些大学教授也用类似方法给学生打分．有时，有必要做出完全“无偏的”决定．在矩阵对策论中，随机性也与最优策略密不可分．

(f) 密码学．在多种保密通信方式中，数据需要保密，无偏的二进位源是至关重要的．

(g) 美学．少许随机性使得计算机生成的图形和音乐更富有生趣．例如在某些情况下，下面左边的模式往往比右边的模式更吸引人．［参阅高德纳，Bull. Amer. Math. Soc. 1 (1979), 369．］

(h) 娱乐．几乎人人都喜欢掷骰子、洗牌、转动轮盘等消遣活动．鉴于随机数的这种传统用法，人们使用“蒙特卡罗方法”一词来泛指一切使用随机数的算法．

考虑随机数的人总是爱陷于“‘随机’一词的含义是什么”的哲学讨论．在某种意义下，所谓“一个随机数”根本不存在．试问，2 是随机数吗？相反，我们说具有特定分布的、独立随机数的序列，意指每个数都是随机得到的，与该序列中的其他数无关，并且每个数都以特定概率落入任意给定的取值范围．

在有限数集上的均匀分布中，每个可能的数都是等可能的．除非另作明确说明，否则分布都视为均匀分布．

在一个（均匀的）随机数字序列中，0 到9 这十个数字的每一个出现的比率都大约是．每两个固定数字出现比率都大约是 ，以此类推．但是，如果我们真的取一个具有一百万位数字的真正随机的序列，那么它并非总是恰好包含100 000 个0，100 000 个1，等等．事实上，这种可能性相当小，许多个这种序列平均起来才会具有这种性质．

所有一百万位数字的序列都具有相同的可能性．因此，如果我们随机选取一百万个数字，并且前999 999 个碰巧都是0，则在真正随机的情况下，最后一个数字恰好为0 的可能性仍然只有 ．许多人会觉得这些话自相矛盾，但实际上它们并无矛盾．

随机性有很多种严格的抽象定义方法，3.5 节将继续讲解这一有趣的主题．现在，我们只需要直观地理解这一概念就足够了．

许多年前，需要随机数的科研工作者会从“充分搅匀的桶”中摸球，或者掷骰子，或者抽牌．1927 年，伦纳德•蒂皮特公布了一张“从人口普查报告中随机抽取”的、超过40 000 位随机数字的表．

自那以后，人们制造了一些设备用来机械地生成随机数．1939 年，莫里斯•肯德尔和伯纳德•巴宾顿–史密斯使用第一台这样的机器，产生了100 000 位随机数字的表．

FerrantiMark I 计算机于1951 年首次投入使用，它有一条内置指令，使用电阻噪声发生器，把20 个随机位送入累加器．此前，图灵曾经建议使用这种做法．

1955 年，美国兰德公司公布了借助另一台特殊设备得到的一百万位随机数字的表，这份数表得到广泛使用．多年来，英国溢价储蓄债券彩票一直使用著名的随机数生成机器ERNIE，用来产生中奖号码．［弗洛伦丝•戴维在《游戏、上帝和赌博》（Games, Gods, and Gambling (1962)）中介绍了早期的历史情况．又见肯德尔和巴宾顿–史密斯，J. Royal Stat. Soc. A101 (1938), 147{166；B6 (1939), 51{61；关于MarkI，见西蒙•拉文顿，CACM 21 (1978), 4{12；关于兰德公司随机数表，见Math. Comp. 10(1956), 39{43；关于ERNIE，见威廉•汤姆森，J. Royal Stat. Soc. A122 (1959), 301{333．］

计算机出现之后不久，人们就开始寻找在计算机程序中得到随机数的高效方法．可以使用一张随机数表，但是这种方法的效用有限，因为需要内存空间和输入时间，表可能太短，制作和维护随机数表也有点麻烦．可以把ERNIE 之类机器连到Ferranti Mark I 之类计算机上，但是事实证明效果并不令人满意，因为测试程序时，不可能正确地重现计算；此外，这种机器容易出现很难检测的故障．

20 世纪90 年代，由于技术进步，可以轻松获得十亿个通过测试的随机字节，因此随机数表再次有了实用意义．1995 年，乔治•马尔萨利亚制作了一张包含650 兆随机字节的演示盘，帮助随机数表复活．这些随机字节来自一个噪声二极管电路的输出，混以经过确定扰码的说唱音乐．（他称之为“黑白噪声”．）

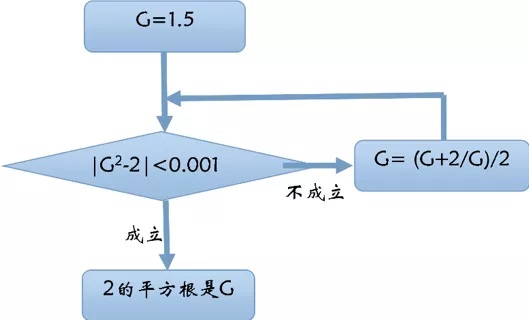
由于早期机械方法的不足，人们开始关注如何使用计算机的普通算术运算产生随机数．大约在1946 年，冯•诺依曼最先提议使用这种方法．他的想法是，取前一个随机数的平方，并取出中间几位数字作为新的随机数．例如，如果我们要生成具有10 位数字的数，已知前一个数是5772156649，则我们求它的平方，得到

33317792380594909201，

于是，下一个数为7923805949．

这种方法的问题很明显：既然每一个数都完全由前一个数所确定，用这种方法生成的序列怎么可能是随机的？（见本章开始处冯•诺依曼的评述．）答案是：这个序列不是随机的，

但是它看上去是．在一般应用中，前后两个数之间虽然有实际联系，但不具有实际影响，因此，非随机性并没有什么实际缺点．直观看来，取平方的中间几位数，已经相当充分地扰乱了前一个数．

在深奥的科技文献中，像这类以确定方法生成的序列，通常称作伪随机（pseudorandom）或准随机（quasirandom）序列．在本书的大部分地方，我们将简单地称它们为随机序列，但要明白它们只是看上去是随机的，反正这或许已经是我们对于随机序列的最高评价了．

在几乎所有的应用中，只要细心选择合适的方法，在计算机上确定地生成的随机数效果都相当好．当然，确定性序列并非总是正确的解，彩票开奖的时候肯定不应该用它取代ERNIE．

事实上，业已证明冯•诺依曼最初的“平方取中法”是一种相对较差的随机数源．危险在于序列容易陷入定式，也就是元素会以短的循环周期重复出现．例如，假如序列中出现一次零，后面就都是零了．

20 世纪50 年代早期，一些人曾用平方取中法进行实验．使用4 位，而不是10 位数字，福赛斯尝试了16 种不同的初值，发现其中12 种导致序列最终陷入循环6100, 2100, 4100, 8100,6100, : : : ，

还有2 种退化为零．尼古拉斯•梅特罗波利斯进行了更全面的测试，主要使用二进制记数系统．结果表明，当使用20 位数时，平方取中法的序列可能退化为13 种不同的循环，最长的周期为142．

如果检测到零，很容易用一个新值重新开始平方取中法；但是长循环没那么容易检测和避免．习题6 和7 讨论了一些有趣方法，使用极少量内存，检测周期序列的循环．

平方取中法的一个理论缺陷在习题9 和10 中给出．另一方面，使用38 位二进制数，梅特罗波利斯得到了一个大约有750 000 个数且尚未退化的序列，结果令人满意，这750 000 × 38位数字通过了随机性的统计检验．［Symp. on Monte Carlo Methods (Wiley, 1956), 29{36．］这一实验表明，平方取中法能够给出有用的结果，但是如果没有精心进行繁复计算，信任这种方法其实相当不稳妥．

在第一次编写本章时，正使用的许多随机数生成器都不太好．人们习惯于回避研究这样的子程序，不怎么令人满意的老方法在程序员中盲目地代代相传，而用户对方法原来的局限性一无所知．本章，我们将会看到，尽管必须足够审慎才能避免常见错误，但是关于随机数生成器的最重要事实并不难把握．

发明一个完美的随机数源并不容易．1959 年，我曾试图用如下方法创建一个想象中的好生成器，因而对此深有体会．

算法K （“超级随机”数生成器）． 给定一个10 位十进制数X，该算法可以把X 改变成想象中的随机序列中的下一个数．尽管该算法预期可以产生相当随机的序列，但是下面给出的理由表明它其实并不太好．（读者不必认真研究该算法，只需注意该算法多么复杂，特别是注意步骤K1 和K2．）

（对应于这个算法的机器语言程序刻意设计得极其复杂，以至于没有附加的注释，人们根本不知道它在做什么．）

算法K 有这么复杂麻烦的步骤，它似乎理应产生几乎无穷多个完全随机的数，是吗？不是的！事实上，当该算法第一次在计算机上运行时，它几乎立即收敛到十位数值6065038420，由于异乎寻常的巧合，该数被算法K 变换到自身（见表1）．使用另一个初值，序列在7401 个值后开始重复，循环周期的长度为3178．

这件事的教训是：随机数不应该用随机选择的方法生成，应该使用某种理论．

在以下几节，我们将考察比平方取中法和算法K 更好的随机数生成器．对应的序列确保具有令人满意的某些随机性质，并且不会出现退化．我们将详细考察这种看似随机的行为的原由，并且考虑随机数的处理方法，例如探讨如何在计算机程序中模拟纸牌的洗牌．

3.6 节总结本章，并且列举一些参考文献源．

本页Url